Filosofia:vastakohtaisuuksien neliö
vastakohtaisuuksien neliö
| vastakohtaisuuksien neliö |
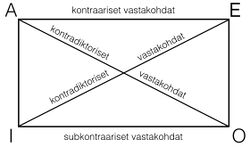
perinteinen tapa jakaa kategoriset arvostelmat neljään luokkaan: A. universaaliset myöntävät, E. universaaliset kieltävät, I. partikulaariset myöntävät ja O. partikulaariset kieltävät
Aristoteleen mukaan yksinkertaisten arvostelmien perusmuoto on ’S on P’, jossa S on subjekti(termi), P on predikaatti(termi) ja sana ’on’ on ns. kopula. Nämä nk. kategoriset arvostelmat voidaan jakaa kvantiteetin mukaan universaalisiin ja partikulaarisiin sekä kvaliteetin mukaan myöntäviin ja kieltäviin. Yhdistämällä erottelut universaalinen-partikulaarinen ja myönteinen-kielteinen saadaan neljä arvostelmien perustyyppiä, jotka muodostavat vastakohtaisuuksien neliön:
A. (Universaalinen, myönteinen) Kaikki S:t ovat P.
E. (Universaalinen, kielteinen) Mitkään S:t eivät ole P.
I. (Partikulaarinen, myönteinen) Jokin S on P.
O. (Partikulaarinen, kielteinen) Jokin S ei ole P.
Arvostelmaparit A ja O sekä E ja I ovat kontradiktorisia vastakohtia, jotka eivät voi olla yhtä aikaa tosia eivätkä yhtä aikaa epätosia. A ja E ovat toistensa kontraariset vastakohdat, jotka eivät voi olla yhtä alkaa tosia, kun taas I ja O ovat subkontraariset vastakohdat, jotka eivät voi olla yhtä aikaa epätosia. Kuviona vastakohtaisuuksien neliö ei esiinny vielä Aristoteleellä (kuten ei myöskään I:n ja O:n subkontraarinen vastakohtaisuus), vaan sen eri versiot ilmaantuvat myöhäisantiikissa 2. vuosisadalta j.a.a. alkaen. Keskiajalle vastakohtaisuuksien neliö, kuten suuri osa muustakin Aristoteleen logiikasta, välittyi Boëthiuksen (480-525 j.a.a.) kirjoitusten ja latinankielisten käännösten kautta.
Erikieliset vastineet
| Square of Opposition | englanti (English) |
Lähikäsitteet
- kategorinen propositio (funktiosuhde)
- kontraarinen vastakohta (osakäsite)
- kontradiktorinen vastakohta (osakäsite)
- subkontraarinen vastakohta (osakäsite)
- traditionaalinen logiikka (kokonaisuuskäsite)
Käytetyt lähteet
Alaviitteet
Lähdeviittaus tähän sivuun:
Tieteen termipankki 21.2.2026: Filosofia:vastakohtaisuuksien neliö. (Tarkka osoite: https://tieteentermipankki.fi/wiki/Filosofia:vastakohtaisuuksien neliö.)