hyperbeli


hyperbeli

Selite Hyperbeli on niiden tason pisteiden joukko, joiden kahdesta polttopisteestä mittattujen etäisyyksien erotus on vakio. Allaolevassa kuvassa polttopisteet on merkitty punaisilla pisteillä.

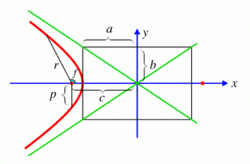
Yhtälö suorakulmaisessa koordinaatistossa on

x² / a² - y² / b² = 1,

missä
a = isoakselin puolikas,
b = pikkuakselin puolikas = a ( e² - 1 )^1/2,
e = eksentrisyys, e > 1

Tämän yhtälön toteuttaa kuvaan piirretyn käyrän lisäksi sen oikealle aukeava peilikuva. Tähtitieteessä on merkitystä vain sillä haaralla, jonka puoleisessa polttopisteessä sijaitsee jokin taivaankappale.

Napakoordinaatistossa yhtälö on

r = p / ( 1 + e cos f ),

missä p on parametri p = a ( e² - 1 ).

Etäännyttäessä origosta hyperbelin haarat lähestyvät kahta suoraa, asymptootteja (kuvan vihreät viivat). Asymptoottien yhtälöt ovat

y = (b / a ) x,
y = -(b / a ) x.

Erikieliset vastineet

hyperbola

englanti (English)

Käytetyt lähteet

Zubenelgenubi

Alaviitteet

Lähdeviittaus tähän sivuun:
Tieteen termipankki 5.11.2024: Tähtitiede:hyperbeli. (Tarkka osoite: https://tieteentermipankki.fi/wiki/Tähtitiede:hyperbeli.)

Siirry tarkastelemaan sivun muokkaushistoriaa →