laukaisuikkuna


laukaisuikkuna

Selite

Radat

Jotta satelliitti tai luotain ei lähdön jälkeen putoaisi takaisin maanpinnalle, sille on annettava riittävän suuri nopeus. Jotta se jäisi Maata kiertävälle radalle, sen nopeuden on oltava ainakin 7,8 kilometriä sekunnissa eli 28 000 kilometriä tunnissa, jolloin se kiertää Maan kerran noin puolessatoista tunnissa.

Jos satelliitti halutaan viedä korkeammalla, sen nostamiseen isommalle radalle tarvitaan lisää energiaa. Samalla kuitenkin ratanopeus pienenee ja kiertoaika pitenee Keplerin lakien mukaisesti. Kun radan säde on runsaat 42 000 km eli korkeus maanpinnasta 36 000 km, kiertoaika on sama kuin Maan pyörähdysaika, joten Maasta katsottuna luotain näyttää pysyvän aina samassa suunnassa (tietenkin se liikkuu tähtien suhteen). Tällaista satelliittia sanotaan geostationaariseksi. Jos rata ei ole päiväntasaajan tasossa tai jos se ei ole täysin pyöreä, satelliitti ei pysy samassa suunnassa, vaan heilahtelee vuorokauden mittaan keskimääräisen paikkansa ympärillä. Tällainen satelliitti on geosynkroninen.

Geostationaarisia ratoja käyttävät esimerkiksi monet tietoliikennesatelliitit. Kun satelliittitelevision lautasantenni suunnataan kerran tällaiseen satelliittiin, sitä ei tarvitse sen jälkeen käännellä, koska satelliitti on aina samassa suunnassa. Geostationaarinen säähavaintosatelliitti puolestaan näkee koko ajan saman alueen Maasta.

Monet tiedustelu-, sää- ja kaukokartoitussatelliitit käyttävät napojen yli kulkevia ratoja. Radan asento säilyy samana, mutta Maa pyörii satelliitin alla, jolloin satelliitti voi tarkkailla koko planeetan pintaa. Valitsemalla radan asento sopivaksi ratataso saadaan myös kiertymään halutulla tavalla häiriöiden vaikutuksesta.

Kolmen kappaleen probleema on kuuluisa taivaanmekaniikan ongelma. Lagrangen pisteet ovat seb erikoisratkaisuja. Maa ja Aurinko yhdessä satelliitin kanssa muodostavat kolmen kappaleen järjestelmän, jonka Lagrangen pisteet kiertävät Aurinkoa samalla nopeudella kuin Maa ja pysyvät siten paikoillaan Maan ja Auringon suhteen. Yksi näistä pisteistä, L1, on Maan ja Auringon välissä. Siihen on sijoitettu Aurinkoa tarkkaileva SOHO-satelliitti. Toinen Lagrangen piste L2 on Maasta katsottuna vastakkaisessa suunnassa kuin Aurinko. Se on pysyvästi Maan varjossa, joten se on sopiva paikka satelliitille, jota Auringon säteily voisi häiritä. Esimerkiksi kosmista mikroaaltosäteilyä tutkiva WMAP on sijoitettu tämän pisteen lähelle.

Jotta luotain voitaisiin lähettää toiselle taivaankappaleelle, sen täytyy päästä pakoon Maan painovoimakentästä. Tähän tarvittava nopeus eli pakonopeus Maan pinnalta on 11 kilometriä sekunnissa.

Sen jälkeen luotaimeen vaikuttaa pääasiassa Auringon painovoima, ja senkin voittaminen vaatii energiaa. Energiaa tarvitaan lähetetäänpä luotain Maan lähistöltä lähemmäs Aurinkoa tai kohti ulompia planeettoja.

Planeettaluotaimen lähettämiseen tarvitaan sitä enemmän energiaa, mitä nopeammin perille on päästävä. Hitaampaan matkaan energiaa tarvitaan vähemmän, mutta on olemassa tietty raja, jota vähemmällä ei selvitä. Essenin kaupungin arkkitehti Walter Hohmann (1880--1945) osoitti jo 1925, että vähiten energiaa kuluu ellipsiradalla, joka perihelissä ja aphelissä sivuaa Maan ja kohteena olevan planeetan ratoja. Tällaisella radalla liikkuva luotain tekee puoli kierrosta Auringon ympäri, joten matkaan kuluu runsaasti aikaa. Esimerkiksi matka Maasta Marsiin pitkin minimienergiarataa kestää runsaat kahdeksan kuukautta.

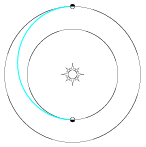
Jotta luotain kohtaisi planeetan tehtyään puoli kierrosta ellipsiradallaan Auringon ympäri, se on laukaistava oikealla hetkellä, tavallisesti muutaman viikon sisällä. Tätä aikaväliä sanotaan laukaisuikkunaksi. Jos lähtö viivästyy, minimienergiarata ei enää vie luotainta planeetan lähistölle, ja silloin on odotettava, kunnes Maan ja planeetan keskinäinen sijainti toistuu taas samanlaisena. Kuten oheisesta luettelosta ilmenee, saman laukaisuikkunan aikana on usein lähetetty kaksi suunnilleen samanlaista luotainta, mikä luonnollisesti parantaa onnistumisen todennäköisyyttä.

Aikanaan luotain lähestyy toista planeettaa suurella nopeudella ja jatkaa matkaansa sen ohi, ellei mitään tehdä. Jos luotaimen halutaan jäävän planeettaa kiertävälle radalle, sen nopeutta on lähestymisvaiheessa jarrutettava, ja taas kuluu energiaa.

Lisää energiaa tarvitaan, jos luotain tai tavallisesti vain sen pieni laskeutumisosa halutaan laskea pehmeästi planeetan pinnalle. Nopeuden vähentämisessä voidaan käyttää apuna planeetan ilmakehän kitkaa. Sillä tavoinhan Maata kiertävät avaruusalukset saadaan takaisin alas; varsin pienellä nopeuden muutoksella aluksen rata muuttuu niin, että se kulkee ilmakehän yläosien kautta, jolloin ilman kitka edelleen hidastaa liikettä ja saa aluksen putoamaan yhä jyrkemmin. Kitkan vaikutuksesta energiaa muuttuu lämmöksi, ja aluksen suojaaminen korkeaksi nousevalta kuumuudelta on vaativa tekninen ongelma.

Jos kohteena olevalla kappaleella on ilmakehä, putoamista jarrutetaan yleensä laskuvarjolla. Viimeisimpien Mars-laskeutujien törmäystä on lisäksi vaimennettu luotainta joka puolelta ympäröivillä ilmatyynyillä. Pinnalle putoava luotain pomppii hetken rantapallon tavoin ennen kuin asettuu aloilleen.

Jos planeetalta halutaan lähettää näyte (tai mukana ollut astronautti) takaisin Maahan, kaikki edellä mainitut toimenpiteet on suoritettava päinvastaisessa järjestyksessä.

Voi tuntua yllättävältä, että aivan Auringon lähelle on vaikeampaa päästä kuin ulos aurinkokunnasta. Luotain saa nimittäin lähdössä mukaansa Maan ratanopeuden, noin 30 kilometriä sekunnissa. Jotta luotain putoaisi Aurinkoon, siltä on otettava pois tämä nopeus, mitä ei nykyisellä tekniikalla pystytä suoraan tekemään.

Tällaiseenkin ongelmaan on ratkaisu. Luotain ohjataan niin, että se ohittaa sopivasti läheltä jonkin planeetan tai muun ison kappaleen. Kyseessä on tavallaan törmäys: planeetta menettää hitusen liike-energiaansa ja siirtää sen luotaimelle (tai päinvastoin). Vaikka kappaleet eivät kosketakaan toisiaan, painovoima välittää niiden vuorovaikutuksen. Planeetan massa on niin paljon suurempi kuin luotaimen, ettei sen liike muutu havaittavasti, vaikka luotaimen nopeus voi muuttua merkittävästi.

Hyvä esimerkki tästä on Voyager 2, joka vieraili kaikkien jättiläisplaneettojen lähistöllä. Jokaisessa ohituksessa se sai lisää nopeutta, jonka turvin se pääsi aina seuraavaan kohteeseensa ja on nyt poistumassa aurinkokunnasta. Menetelmää on käytetty lukuisia kertoja, jotta luotain on saatu kohteeseensa mahdollisimman pienellä energiamäärällä ja siten edullisesti. Tehokkaiden tietokoneiden avulla erilaisia ratavaihtoehtoja voidaan tutkia helposti, ja joidenkin luotainten radat ovat hämmästyttävän mutkikkaita kiemuroita eri taivaankappaleiden pelatessa luotaimella kosmista biljardia.

Luotausraketit

Laitteita ei välttämättä tarvitse viedä kiertoradalle, vaan ne voidaan vain nostaa raketin avulla ilmakehän yläpuolelle, josta ne sitten putoavat takaisin.

Tieteelliseen kokeeseen rakettia käytettiin ilmeisesti ensi kerran 1822, jolloin ilmassa räjäytetyn raketin suunta havaittiin Wienistä ja Neustadtista. Havainnoista voitiin määrittää paikkakuntien pituusaste-ero.

Toisen maailmansodan jälkeen raketteja alettiin käyttää myös tähtitieteellisiin havaintoihin. Avaruustähtitieteen voinee katsoa alkaneen 10.10.1946, jolloin spektrometri vietiin V-2 -raketilla ilmakehän yläpuolelle ja sillä havaittiin ensi kerran Auringon ultraviolettispektriä.

Vastaavia luotausraketteja käytetään edelleenkin, jonkin verran myös tähtitieteellisiin havaintoihin. Kun havaintolaitteelle ei tarvitse antaa niin suurta nopeutta, että se jäisi Maata kiertävälle radalle, energiaa ei tarvita kovin paljoa ja raketti voi olla yksinkertaisempi. Haittana on tietysti, että havaintoja voidaan tehdä vain muutaman minuutin ajan. Menetelmä sopii kuitenkin esimerkiksi uudentyyppisten havaintolaitteiden kokeiluun ennen kuin ruvetaan rakentamaan kallista avaruuteen jäävää versiota.

Havaintosatelliitit

Avaruudessa liikkuvien satelliittien merkittävin etu on, että havaintoja voidaan tehdä kaikilla sähkömagneettisen säteilyn aallonpituuksilla, joista vain pieni osa pääsee maanpinnalle. Tämä on laajentanut tavattomasti tietoa tähtitaivaan kohteista. Suurienergisissä prosesseissa, kuten kvasaareissa, supernovissa ja mustien aukkojen ympärillä, syntyy lyhytaaltoista säteilyä, joka ei pääse ilmakehän läpi. Myös näkyvää valoa pitempiaaltoinen infrapuna- ja mikroaaltosäteily imeytyy ilmakehän vesihöyryyn. Tämä pitkäaaltoinen säteily on kiinnostavaa mm. tähtienvälisen aineen ja tähtien syntyalueiden tutkimisessa.

Satelliittien avulla päästään eroon myös näkyvän valon havaintoja häiritsevistä ongelmista (ks. ilmakehän vaikutus havaintoihin). Avaruudessa ilmakehän väreily ei heikennä kuvan laatua ja erotuskyky riippuu vain kaukoputkesta ja ilmaisimesta. Jos objektiivin muoto on oikea, suurellakin kaukoputkella saavutetaan sen teoreettinen erotuskyky. Tosin tätä ongelmaa on nykyisin pystytty merkittävästi vähentämään adaptiivisella optiikalla, jolloin maanpäällisilläkin teleskoopeilla päästään lähelle niiden teoreettista erotuskykyä ja huomattavasti halvemmalla kuin avaruusteleskoopeilla.

Näkyvän valon alueella toimivia avaruusteleskooppeja on tällä hetkellä vain yksi, Hubble Space Telescope (HST), jossa on 2,4 metrin peili. Optiikkaa ei testattu kunnolla etukäteen, ja se osoittautui vialliseksi teleskoopin ollessa jo kiertoradalla. Sukkulalennolla teleskooppiin asennettiin korjausoptiikkaa, jolla erotuskyky saatiin paremmaksi. Tähtien kuvat leviävät silti mutkikkaiksi diffraktiokuvioiksi, joiden vuoksi esimerkiksi tähtien kirkkauksien mittaaminen on erittäin vaikeaa. HST menetti näin osan etulyöntiasemastaan.

Maanpinnalta tehtäviä havaintoja vaivaa myös ilmasta siroava valo, jonka lähteitä ovat päivällä Aurinko ja yöllä valosaaste, Kuu ja myös tähdet. Tämän sironneen valon vuoksi taustataivas ei ole musta, jolloin himmeät kohteet eivät erotu. Avaruudessa hajavaloa ei ole ja taivas on musta päivälläkin, joten havaintoja voidaan tehdä jatkuvasti.

Avaruuden etuna on myös rajaton tila. Maanpäällisten teleskooppien välimatka ei voi olla Maan läpimittaa suurempi, mikä rajoittaa interferometristen havaintojen tarkkuutta. Tämä rajoitus poistuu, jos havaintolaitteet viedään avaruuteen. Teleskooppien välimatka voi olla melkein miten suuri tahansa, jolloin voidaan jo havaita niinkin pieniä yksityiskohtia kuin Maan kokoisia planeettoja muista aurinkokunnista.

Kun havaitaan ultraviolettia pitempiä aallonpituuksia, avaruudessa toimiva teleskooppi on periaatteeltaan samanlainen kuin maanpäällinenkin optinen tai radioteleskooppi. Lyhemmät aallonpituudet sen sijaan eivät heijastu peilistä tai taitu linssissä, vaan absorboituu ja pysähtyy niihin. Siksi niiden havaitsemiseen tarvitaan aivan toisenlaisia laitteita. Ks. röntgen- ja gammasädehavainnot.

Röntgensatelliitti Chandran erotuskyky on jo yhtä hyvä kuin maanpäällisillä optisilla teleskoopeilla. Gammasäteilyn havainnoissa ollaan vielä jäljessä, mutta epäilemättä niidenkin tarkkuus paranee huomattavasti lähivuosina.

Planeettaluotaimet

Kuuta tutkittaessa käytettiin aluksi törmäysluotaimia, jotka vain osuivat Kuun pintaan, sitten laskeuduttiin pehmeästi pinnalle ja tutkittiin Kuuta kiertoradalta. Viimeinen vaihe oli näytteiden palauttaminen Maahan. Samalla tavoin voidaan jakaa aurinkokuntamme muitakin kappaleita tutkivat luotaimet. Törmäysluotaimia tosin ei käytetä, vaan kalliin laitteen halutaan toimivan mahdollisimman pitkään. Niiden tilalla ovat luotaimet, jotka ohittavat kohteensa läheltä, mutteivät jää sitä kiertämään.

Törmäys- ja ohitusluotaimet tarvitsevat vähiten energiaa. Kiertoradalle pääsy on jo vaikeampaa ja laskeutuminen kaikkein hankalinta.

Jonkinlaiset luotaimet ovat tutkineet jo kaikkia muita planeettoja paitsi Plutoa. Toistaiseksi Merkuriusta, Uranusta ja Neptunusta on tarkkailtu vain ohilennoilta. Venuksen, Marsin, Jupiterin ja viimeksi Saturnuksen kiertoradoille on lähetetty luotaimia. Pehmeä lasku on suoritettu lähimpien planeettojen, Venuksen ja Marsin, sekä Saturnuksen kuun Titanin pinnalle.

Luotaimilla on tutkittu myös muutamaa komeettaa ja asteroidia. Myös yhden asteroidin, Eroksen, pinnalle on laskeuduttu. Asteroidin tapauksessa laskeutumisen ongelmana on nopeuden pitäminen todella pienenä. Pakonopeus asteroidin pinnalta on niin olematon, että sieltä pääsisi pois hyppäämällä. Jotta luotain asettuisi pinnalle, se ei saa töyssyä yhtään kosketushetkellä.

Toistaiseksi vain Kuusta on saatu näytteitä tutkittavaksi, ja Kuu on myös ainoa vieras taivaankappale, jolla ihminen on käynyt. Seuraavaksi lähin suuri taivaankappale on Venus, mutta olosuhteet sen pinnalla tekevät siitä liian vaikean kohteen. Niinpä luonnollinen valinta avaruuden valloituksen seuraavaksi kohteeksi on Mars. Sen massa on melko pieni, joten laskeutumiseen tarvittava energiamäärä ei ole kohtuuton. Miehitettyyn lentoon kulunee vielä useita vuosikymmeniä, mutta näytteitä saadaan varmaankin jo paljon aikaisemmin.

Planeettaluotaimet vaativat pitkäjännitteisyyttä. Luotaimen suunnittelu ja rakentaminen vie useita vuosia. Kuorman paino on hyvin rajoitettu, joten ensin on mietittävä, mitä tietoja kaikkein kipeimmin halutaan ja millaisia laitteita mukaan saadaan mahtumaan. Laitteet on rakennettava mahdollisimman pieniksi, mutta niin, että ne kestävät vuosikausia avaruuden äärimmäisiä olosuhteita. Kun luotain sitten lopulta lähtee, sen matka voi kestää vuosikausia ja se voi joutua kiertelemään mutkikasta rataa useiden planeettojen kautta ottamassa lisää vauhtia. Jos kyseessä on ohilento, varsinainen havaintojakso kestää ehkä vain muutaman tunnin, vaikka sen valmisteluun on hyvinkin voinut mennä vuosikymmen. Tuon lyhyen ohituksen aikana on kerättävä mahdollisimman paljon tietoa, jossa tutkijoille sitten riittää pureksittavaa seuraavien vuosien ajaksi.

Erikieliset vastineet

launch window	englanti (English)
spaceflights	englanti (English)
theory	englanti (English)

Käytetyt lähteet

Zubenelgenubi

Alaviitteet

Lähdeviittaus tähän sivuun:
Tieteen termipankki 22.11.2024: Tähtitiede:laukaisuikkuna. (Tarkka osoite: https://tieteentermipankki.fi/wiki/Tähtitiede:laukaisuikkuna.)

Siirry tarkastelemaan sivun muokkaushistoriaa →