interpolointi


interpolointi

Määritelmä jonkin suureen tunnettujen tai taulukoitujen arvojen välissä olevien arvojen laskeminen

Selite

Esimerkiksi tähtitieteellisissä vuosikirjoissa annetut planeettojan koordinaatit on ilmoitettu vain yhden tai useamman päivän välein. Jos muutokset ovat hitaita, voit arvioida koordinaatit mielivaltaiselle hetkelle olettamalla, että noiden kahden hetken välillä koordinaatti muuttuu tasaisella nopeudella. Tätä taulukkoarvojen väliin jäävien lukujen arviointia tarkoittaa interpolointi. Jos oletat muutoksen tasaiseksi, kyseessä on lineaarinen interpolointi.

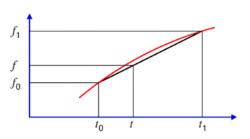
Oletetaan, että taulukossa on ilmoitettu jonkin suureen arvot hetkille t₀ ja t₁, ja haluat sen hetkelle t, joka on näiden välissä. Jos suureen arvo hetkellä t₀ on f₀ ja hetkellä t₁ f₀, sen arvo hetkellä t on likimain

f = f₀ + [ (t - t₀) / (t₁ - t₀) ] (f₁ - f₀).

Esimerkki: Tähdet 1993 -kirjan taulukon mukaan Marsin rektaskensio 23.4. tunneiksi muutettuna oli 8.038 ja 9.5. 8.575 tuntia. Mikä oli sen rektaskensio 2.5?

Aikavälit vuorokausina ovat t₁ - t₀ = 16 ja t - t₀ = 9. Saamme siis rektaskensioksi

8.038 + (9 / 16) (8.575 - 8.038) = 8.340.

Vastaava menetelmä soveltuu toki myös taulukoihin, joissa muuttujana ei ola aika, vaan jokin muu suure. Mikäli muutos ei ole tasaista tai tarvitaan suurempaa tarkkuutta, voidaan käyttää useamman pisteen interpolaatiota. Mistä tahansa numeerisen analyysin oppikirjasta löytyy suuri määrä erilaisiin tilanteisiin soveltuvia menetelmiä.

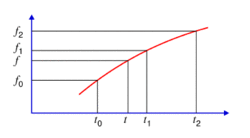
Seuraava kolmeen pisteeseen perustuva kvadraattinen interpolointi on lineaarisen interpoloinnin yksinkertaisin täsmennys. Siinä laskettavaa suuretta kuvataan toisen asteen käyrällä. Esimerkiksi planeettojen koordinaateille tällainen menetelmä antaa jo hyvin tarkat arvot.

Oletetaan, että hetkiä t₀, t₁ = t₁ + h ja t₂ = t₁ + 2h vastaavat muuttujan arvot ovat f₀, f₁ ja f₂. Nämä taulukkoarvot on valittu siten, että t₁ on lähinnä haluttua hetkeä t.

Lasketaan aluksi interpolointivälin suhde taulukointiväliin:

d = (t - t₁) / h.

Muuttujan arvo hetkellä t on silloin

f = f₁ + (f₂ - f₀) d / 2 + (f₂ - 2f₁ + f₀) d² / 2

Esimerkki: Lasketaan edellisen esimerkin mukainen Marsin paikka tarkemmin, kun tiedämme, että 25.5 sen rektaskensio oli 9.135 tuntia.

Ensinnäkin saamme

d = (2 - 9) / 16 = -0.4375.

Rektaskensio on siten

8.575 - (9.135 - 8.038)(0.4375 / 2) + (9.135 - 2×8.575 + 8.038) 0.4375²/2 = 8.337.

Kolmen pisteen interpolointi antaa esimerkiksi planeettojen koordinaatit riittävän tarkasti useimpiin tarkoituksiin, jos taulukoidut arvot on annettu vuorokauden välein. Käyttämällä vielä useampia pisteitä, saadaan yhä tarkempia interpolointikaavoja, mutta samalla ne tulevat mutkikkaammiksi ja niiden laskeminen käy hitaammaksi.

Erikieliset vastineet

interpolation

englanti (English)

Käytetyt lähteet

Zubenelgenubi

Alaviitteet

Lähdeviittaus tähän sivuun:
Tieteen termipankki 22.11.2024: Tähtitiede:interpolointi. (Tarkka osoite: https://tieteentermipankki.fi/wiki/Tähtitiede:interpolointi.)

Siirry tarkastelemaan sivun muokkaushistoriaa →