ilmanpaine

Selite Paine kuvaa kappaleen pinta-alayksikköä kohti kohdistuvaa voimaa. SI-järjestelmässä paineen yksikkö on pascal:

1 Pa = 1 N / m².

Paksuhkoa paperia sisältävän laatikon kyljessä voi olla merkintä "100 g". Se tarkoittaa, että yksi neliömetri kyseistä paperia painaa 100 grammaa eli 0.1 kilogrammaa (siis oikeastaan sen massa on 100 grammaa), joten se kohdistaa alustaansa 0.98 Newtonin voiman. Vaakasuorassa lepäävä tasaiseksi levitetty arkki tällaista paperia pusertaa alustaansa melkein yhden pascalin paineella. Pascal on siis varsin pieni yksikkö.

Paineelle käytetään yleisesti useita muitakin yksiköitä. Niiden käyttöä ei suositella, mutta niitä kohtaa melko usein, joten on hyvä tietää, miten ne voi muuntaa standardin mukaisiksi SI-yksiköiksi.

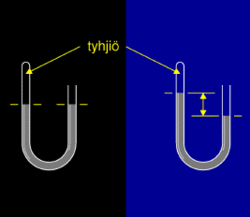
Ilmanpainetta voidaan mitata U:n muotoisella toisesta päästä suljetulla putkella, joka sisältää nestettä. Kun putki on tyhjiössä, nesteen pinta asettuu samalle tasolle putken molemmissa haaroissa. Jos avoimen pään kautta nesteen pintaan kohdistuu painetta, se työntää nestettä putken toiseen haaraan. Nestepintojen välimatka on verrannollinen ilmanpaineeseen. Mittaamalla ylemmän nestepinnan etäisyys alemmasta saadaan selville nesteeseen vaikuttava paine. Periaatteessa tällaisessa ilmapuntarissa voisi käyttää mitä tahansa nestettä. Kevyttä nestettä käytettäessä ongelmana on nestepatsaan pieni paino, minkä vuoksi se kohoaa hyvin korkealle ja vaatii pitkän putken. Käytännössä ilmapuntareissa käytetäänkin vain elohopeaa, jolloin laitteen koko pysyy kohtuullisena.

Tällaiseen paineen mittausmenetelmään perustuu elohopeamillimetri eli torri. Se on paine, jonka yhden millimetrin paksuinen elohopeakerros aiheuttaa pohjapintaa vastaan. Koska elohopean tiheys riippuu lämpötilasta, sovitaan, että lämpötila on 0°C. Tietyn elohopeamäärän massa on kyllä kaikkialla vakio, mutta sen paino riippuu vetovoiman kiihtyvyydestä. Siksi täytyy vielä sopia, että kyseessä on tietty normipaikkakunta.

Torri on saanut nimensä italialaisen matemaatikon, Galilein työtoverin, Evangelista Torricellin (1608--1647) mukaan. Torricelli osoitti kokeillaan ilmakehän paineen vaikutuksen ja havaitsi myös paineen vaihtelun. Torricelli käytti U-putken sijasta suoraa toisesta päästä suljettua putkea, joka täytettiin elohopealla. Kun sen avoin pää upotettiin myös elohopeaa sisältävään maljaan, putkessa olevan nesteen yläpinta asettui noin 760 mm maljassa olevan nesteen pintaa ylemmäksi.

Elohopeailmapuntarin periaate. Jos ilmapuntari on tyhjiössä (vasemmalla), elohopeapinta asettuu putken kummassakin haarassa samalle tasolle. Kun putken avoimeen päähän vaikuttaa ilman paine (oikealla), se työntää elohopeaa putken toiseen päähän. Nestepintojen korkeusero ilmoittaa paineen.

Ilmakehä aiheuttaa suurin piirtein 760 torrin paineen. Normaali-ilmakehä (atm) onkin määritelty juuri 760 torriksi.

Jos nesteenä käytettäisiin elohopean sijasta vettä, ilman paine työntäisi sen noin 10 metrin korkeuteen. Ilmakehän paine puristaa meitä siis samalla voimalla kuin tyhjiössä oleva 10 metrin paksuinen kerros vettä.

Kaivojen rakentajat tietävät (tai ainakin heidän olisi syytä tietää), että tämä 10 metriä aiheuttaa omat rajoituksensa vesipumpuille. Imupumppu ei varsinaisesti nosta vettä, vaan se aiheuttaa putken sisälle alipaineen, ja ulkopuolisen ilman paine työntää sitten vettä putkeen. Jos imupumppu on täysin tiivis ja täydellinen, se muodostaa imupuolella olevaan putkeen tyhjiön. Ilman paineen vuoksi vesi nousee tässä tyhjiössä korkeintaan 10 metrin korkeuteen. Imupumpulla vettä voi siten nostaa korkeintaan 10 metrin syvyydestä. Jos vettä on nostettava syvemmältä, on käytettävä esimerkiksi imu- ja työntöpumppua, joka asennetaan maanpinnan alapuolelle.

Varsinkin Yhdysvalloissa käytetään ilmanpaineen ilmoittamiseen elohopeamillimetrien sijasta elohopeatuumaa (inHg). Muissa yhteyksissä tavallisin yksikkö puolestaan on naulaa neliöjalkaa kohti (lbf / ft²). Tässä esiintyvä naula (pound force, lbf) pitäisi kai suomentaa voimanaulaksi tai naulan voimaksi, sillä se ilmoittaa voiman, jolla Maa vetää puoleensa yhden naulan massaista kappaletta.

Paineen yksikkö cgs-järjestelmässä on dyneä neliösenttimetriä kohti. Maanpäällisiä olosuhteita ajatellen tämä on hyvin pieni yksikkö, joten sen sijasta käytetäänkin usein baaria (bar), joka on 10⁶ dyn / cm² tai vielä useammin millibaaria (mb), joka on 1000 dyn / cm². Normaali-ilmakehän paine on noin 1013 mb.

SI-yksiköissä 1 mb on 100 pascalia eli yksi hehtopascal (hPa). Säätiedotuksissa on perinteisesti käytetty yksikkönä millibaaria. Nykyisin käytetään sen sijasta hehtopascalia, jolloin lukuarvot pysyvät samoina. SI-standardin mukaan tällaisen kerrannaisyksikön käyttö ei kuitenkaan ole suositeltavaa, joten parempi olisi siirtyä esimerkiksi kilopascaleihin. Ilmanpaineet olisivat 100 kilopascalin paikkeilla.

Normaali ilmanpaine vastaa siis painetta, jolla 100 000 päällekkäin pinottua arkkia 100-grammaista paperia painaa alustaansa. Sellainen määrä sisältyy 200 kappaleeseen tavallisia 500 arkin pakkauksia.

Maan vetovoima vetää ilmakehää puoleensa. Sen vuoksi me täällä ilmakehän pohjalla asuvat olennot tunnemme niskassamme ilmakehän painollaan aiheuttaman paineen. Jos sukellamme merten syvyyksiin, meitä rusentaa lisäksi yläpuolellamme olevan veden paine. Tässä on kyseessä staattinen paine p_s, jonka meitä ympäröivä aine aiheuttaa pelkällä painollaan.

Jos työntää kätensä ulos liikkuvan auton ikkunasta, huomaa helposti ilmavirrasta aiheutuvan paineen. Paine on sitä suurempi, mitä nopeammin auto liikkuu. Oleellista on virtauksen nopeus suhteessa painetta aistivaan kohteeseen. On yhtä vaikeaa pysyä 100 km/h liikkuvan auton lavalla kuin seisoa paikoillaan 100 km/h puhaltavassa myrskyssä. Erotukseksi edellä esiintyneestä staattisesta paineesta kutsumme tätä virtauksesta aiheutuvaa painetta patopaineeksi tai dynaamiseksi paineeksi.

Dynaaminen paine on sukua liike-energialle, ja sen lauseke saadaankin liike-energian lausekkeesta vaihtamalla massan sijalle virtaavan aineen tiheys rho:

p_d = (1 / 2) rho v ².

Dynaaminen paine on siis verrannollinen virtausnopeuden v neliöön, joten se kasvaa nopeasti nopeuden lisääntyessä.

Staattisen ja dynaamisen paineen summa on kokonaispaine. Jos tarkastellaan paineen käyttäytymistä tietyn kitkattoman virtauksen eri kohdissa, sen havaitaan noudattavan Bernoullin lakia

p_s + p_d = vakio

Jos virtausnopeus on pieni, myös patopaine on pieni, joten suurin osa paineesta aiheutuu staattisesta paineesta. Nopeuden kasvaessa patopaineen osuus kasvaa ja staattinen paine pienenee.

Korkeusmittarit ovat useimmiten ilmapuntarin tapaisia painemittareita, jotka mittaavat staattista painetta. Niissä paineasteikko vain on korvattu vastaavalla korkeusasteikolla. Tällaisen korkeusmittarin lukemat muuttuvat siis paitsi korkeuden myös sään myötä. Siksi mittarin nollakohtaa on voitava säätää, toisin kuin ilmapuntarissa.

Lentokoneiden korkeusmittareissa käytetään pääasiassa kahta erilaista asetusta. Matalalla liikuttaessa mittari säädetään niin, että se näyttää korkeutta keskimääräisestä merenpinnasta. Tällaista asetusta tarkoittaa kryptinen lyhenne QNH. Kentällä näin säädetty mittari osoittaa kentän korkeutta merenpinnasta. Koska kartoissa esiintyvät korkeudet on ilmoitettu juuri merenpinnan suhteen, vilkaisu korkeusmittariin kertoo heti, onko korkeutta riittävästi maaston muodostumien ja antennimastojen ylittämiseen. Korkeammalla mittari asetetaan näyttämään etäisyyttä pinnasta, jolla paine on 1013.2 hPa. Tämä vastaa keskimääräistä merenpintaa normaaliolosuhteissa, mutta ilmanpaineen vaihdellessa myös tämän nollakohdan todellinen korkeus vaihtelee. Etuna on, että pitkällä matkalla mittarin asetusta ei tarvitse jatkuvasti säätää paikallisten olosuhteiden mukaiseksi, ja kaikki kohdattavat koneet mittaavat korkeutensa varmasti täsmälleen samalla tavalla.

Edellinen menetelmä soveltuu myös autoissa käytettäviin korkeusmittariin. Esimerkiksi topografikartasta saadaan selville tietyn paikan täsmällinen korkeus, joka sitten säädetään mittariin. Säätö on tarkistettava aika ajoin, koska mittarin lukema muuttuu myös sääilmiöistä johtuvan ilmanpaineen vaihtelun mukana.

Lentokoneiden nopeusmittarit ovat Bernoullin lain sovelluksia: ne mittaavat kokonaispaineen ja staattisen paineen erotusta, siis dynaamista painetta, josta nopeus voidaan laskea. Tällainen laite ilmoittaa nopeuden ilman suhteen, mikä lento-ominaisuuksien kannalta onkin juuri oleellisin tieto. Nopeus maan suhteen voidaan laskea, jos tunnetaan ilman liike eli tuulen nopeus ja suunta maan suhteen.

Erikieliset vastineet

atmospheric pressure

englanti (English)

Käytetyt lähteet

Zubenelgenubi

Alaviitteet

Lähdeviittaus tähän sivuun:
Tieteen termipankki 19.4.2024: Tähtitiede:ilmanpaine. (Tarkka osoite: https://tieteentermipankki.fi/wiki/Tähtitiede:ilmanpaine.)

Siirry tarkastelemaan sivun muokkaushistoriaa →