hydrostaattinen tasapaino


hydrostaattinen tasapaino

Selite Vetovoima pyrkii puristamaan kokoon kaasua, esimerkiksi ilmakehää tai tähteä. Lämpöliike aiheuttaa paineen, joka puolestaan pyrkii laajentamaan kaasua. Hydrostaattisessa tasapainossa nämä vastakkaissuuntaiset voimat ovat yhtä suuria.

Tästä tasapainoehdosta saadaa hydrostaattisen tasapainon yhtälö, jonka ratkaisuna saadaan esimerkiksi ilmakehän paineen ja korkeuden välinen riippuvuus. Yhtälö on myös yksi tähtien rakennetta kuvaavista perusyhtälöistä.

Hydrostaattisen tasapainon yhtälö

Tarkastellaan ilmakehän rakennetta pystysuunnassa. Siihen vaikuttaa luonnollisesti kaasun koostumus: mitä kevyempiä molekyylit ovat, sitä heikommin planeetan vetovoima niihin vaikuttaa. Toinen tekijä onkin juuri tuo vetovoima. Massiivisen planeetan voimakas vetovoimakenttä vetää kaasua tehokkaammin kohti planeettaa kuin kevyen planeetan kenttä.

Vetovoima pyrkii puristamaan ilmakehää kokoon. Ilmakehän molekyylien liikkeistä aiheutuva paine puolestaan pyrkii laajentamaan ilmakehää, ja siten estää ilmakehän luhistumisen. Ilmakehän rakenne on seurausta siitä, että nämä kaksi vastakkaisiin suuntiin vaikuttaa voimaa ovat tasapainossa. Tätä tasapainoa sanotaan hydrostaattiseksi tasapainoksi.

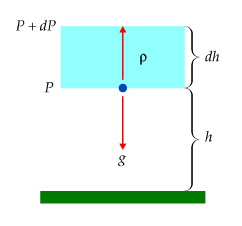
Hydrostaattisessa tasapainossa hiukkaseen vaikuttava vetovoima ja paine-erosta aiheutuva voima kumoavat toisensa.

Tarkastellaan korkeudella h olevaa pientä tilavuusalkiota, jonka korkeus on dh. Olkoon paine alareunalla P ja yläreunalla P+dP. Jos kaasun tiheys on rho, kyseisen tilavuusalkion aiheuttama paine on g rho dh, missä g on vetovoiman kiihtyvyys. Tasapainotilassa paineen muutoksen dP on kumottava juuri tämä paine:

dP = - g rho dh.

Miinusmerkki johtuu siitä, että paine pienenee ylöspäin, joten sen muutos dP on vastakkaissuuntainen kuin korkeuden muutos dh. Tämä on hydrostaattisen tasapainon yhtälön perusmuoto.

Vetovoiman kiihtyvyys g pienenee korkeuden kasvaessa. Laskettaessa tähden tai hyvin paksun ilmakehän rakennetta, tämä riippuvuus on otettava huomioon.

Esimerkiksi Maan ilmakehä on niin ohut, että kiihtyvyys muuttuu siinä vain hyvin vähän. Silloin tilannetta voidaan yksinkertaistaa olettamalla, että g on vakio. Kun vielä käytetään ideaalikaasun yhtälöä, saadaan ratkaisuksi, että paine korkeudella h on

P = P₀ e^-h/H.

Tässä P₀ on paine maanpinnalla ja

H = kT / mg,

missä m on kaasumolekyylin massa ja k Boltzmannin vakio. Pituuden laatuinen suure H on nimeltään skaalakorkeus. Se on korkeus, jossa paine on pudonnut e:nteen osaan pinnalla vallitsevasta paineesta.

Erikieliset vastineet

hydrostatic equilibrium

englanti (English)

Käytetyt lähteet

Zubenelgenubi

Alaviitteet

Lähdeviittaus tähän sivuun:
Tieteen termipankki 15.11.2024: Tähtitiede:hydrostaattinen tasapaino. (Tarkka osoite: https://tieteentermipankki.fi/wiki/Tähtitiede:hydrostaattinen tasapaino.)

Siirry tarkastelemaan sivun muokkaushistoriaa →