Tähtitiede:eksentrinen anomalia
eksentrinen anomalia
| eksentrinen anomalia |
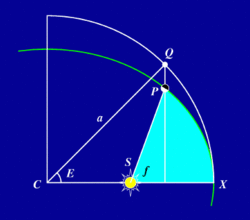
Eksentrisen anomalian määritelmä ilmenee allaolevasta kuvasta. S on Aurinko, P planeetta, joka liikkuu ellipsiradalla (vihreä käyrä). Radan keskipiste on C ja isoakselin puolikas a. Planeetan paikka projisoidaan C-keskiselle ympyräradalle pisteeseen Q, jolloin kulma SCQ on eksentrinen anomalia E Todellinen anomalia f on kulma XSP.
Keskianomalia M saadaan suoraan ajan lausekkeena. Eksentrinen anomalia E voidaan ratkaista Keplerin yhtälöstä
E - e sin E = M,
missä e on radan eksentrisyys. Ratkaisua ei voi esittää äärellisenä lausekkeena. Tämä on se syy, jonka vuoksi planeetan paikkaa ei voi lausua millään yksinkertaisella tavalla ajan lausekkeena. Eksentrinen anomalia voidaan kyllä helposti ratkaista numeerisesti tai esittää sarjakehitelmänä.
Eksentrisestä anomaliasta saadaan luonnollinen anomalia f muunnoskaavoista
cos f = (cos E - e ) / (1 - e cos E ),
sin f = (1 - e 2)1/2 sin E / (1 - e cos E ).
Vaikka eksentrinen anomalia on melko keinotekoisen tuntuinen suure, se yksinkertaistaa huomattavasti ellipsirataan liittyvää matematiikkaa.
Planeetan paikka suorakulmaisessa Aurinkokeskisessä koordinaatistossa, jonka x-akseli osoittaa planeetan perihelin suuntaan, on
x = a (cos E - e),
y = b sin E.
Planeetan etäisyys Auringosta on
r = a (1 - e cos E ).
Erikieliset vastineet
| eccentric anomaly | englanti (English) |
Lähikäsitteet
- anomalia (yläkäsite)
Käytetyt lähteet
Alaviitteet
Lähdeviittaus tähän sivuun:
Tieteen termipankki 17.1.2026: Tähtitiede:eksentrinen anomalia. (Tarkka osoite: https://tieteentermipankki.fi/wiki/Tähtitiede:eksentrinen anomalia.)