pallokolmio


pallokolmio

Selite Jos pallon keskipisteen kautta asetetaan taso, se leikkaa pallon kahteen yhtä suureen osaan pitkin ympyräviivaa, jota sanotaan isoympyräksi. Kahden pallon pinnalla olevan pisteen kautta kulkee täsmälleen yksi isoympyrä (paitsi, jos pisteet ovat vastakkaisilla puolilla palloa, jolloin kaikki näiden pisteiden kautta kulkevat ympyrät ovat isoympyröitä). Tämän isoympyrän kaari on lyhin pallon pinnalla oleva reitti pisteiden välillä.

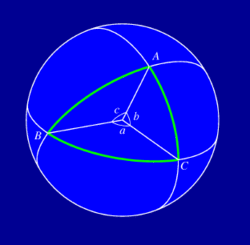
Pallokolmio ei ole mikä tahansa pallon pinnalla oleva kolmikulmainen kuvio, vaan sen sivujen on oltava isoympyrän kaaria. Oheisen kuvan pallokolmiossa ABC ovat sivuina kaaret AB, BCC ja ACC. Jos pallon säde on r, on esimerkiksi kaaren AB pituus

AB = r c, [c] = rad,

missä c on kulma, jossa kaari AB näkyy pallon keskipisteestä. Tätä kulmaa voidaan sanoa sivun AB keskuskulmaksi. Koska sivujen pituudet ja keskuskulmat vastaavat toisiaan yksikäsitteisesti, ilmoitetaan pallokolmion sivujen pituuksien sijasta aina niitä vastaavat keskuskulmat, jolloin pallon säde ei esiinny missään pallotrigonometrian kaavoissa.

Pallokolmion kulma voidaan määritellä esimerkiksi kolmion kärkeen sivuille piirrettyjen tangenttien välisenä kulmana. Tämä kulma on toisaalta sama kuin sivujen ja pallon keskipisteen kautta asetettujen tasojen välinen kulma. Pallokolmion kulmia merkitään seuraavassa isoilla kirjaimilla (A, B, C) ja niiden vastaisia sivuja tai oikeammin näitä sivuja vastaavia keskuskulmia pienillä kirjaimilla (a, b, c).

Tasokolmion kulmien summa on 180°, joten kaksi kulmaa määrää kolmion muodon täydellisesti. Pallokolmiolle tämä ei päde, sillä sen kulmien summa on aina suurempi kuin 180°; ylimäärä on nimeltään palloeksessi. Kahden kulman tunteminen ei vielä riitä määräämään kolmatta kulmaa.

Pallotrigonometria on matematiikan ala, joka tutkii pallokolmioiden sivujen ja kulmien laskemista.

Erikieliset vastineet

spherical triangle

englanti (English)

Käytetyt lähteet

Zubenelgenubi

Alaviitteet

Lähdeviittaus tähän sivuun:
Tieteen termipankki 15.11.2024: Tähtitiede:pallokolmio. (Tarkka osoite: https://tieteentermipankki.fi/wiki/Tähtitiede:pallokolmio.)

Siirry tarkastelemaan sivun muokkaushistoriaa →