Tähtitiede:Keplerin yhtälö

Keplerin yhtälö

Keplerin yhtälö

Selite Keplerin yhtälö liittää toisiinsa ajan ja eksentrisen anomalian (allaolevan kuvan kulma E). Yhtälö joudutaan ratkaisemaan jollakin numeerisella menetelmällä. Likimääräinen ratkaisu saadaan myös sarjakehitelmistä.

Yhtälön johto

Keplerin toisen lain mukaan pintanopeus on vakio, joten kuvan vaaleansinisen alueen pinta-ala on

A = pi ab (t-t₀) / P,

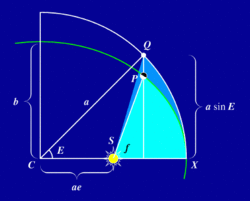
missä t-t₀ on perihelin ohituksesta kulunut aika ja P planeetan kiertoaika. Toisaalta ellipsin eri osien pinta-alat saadaan vastaavien ympyrän osien pinta-aloista pienentämällä niitä ellipsin akselien suhteella b/a. Niin ollen alueen SPX pinta-ala on

A = b/a (SQX:n pinta-ala)
= b/a (sektorin CQX ala - kolmion CQS ala)
= b/a [(1/2)a a E - (1/2) ae a sin E ]
= (1/2) ab (E - e sin E).

Asettamalla nämä pinta-alan lausekkeet yhtä suuriksi saadaan Keplerin yhtälö

E - e sin E = M,

missä

M = 2 pi (t-t₀) / P,

on planeetan keskianomalia hetkellä t.

Huomaa, että e sin E on paljas luku. Siksi muidenkin yhtälössä esiintyvien termien on oltava sellaisia. Kulmat M ja E on siis ehdottomasti lausuttava radiaaneina!

Yhtälön ratkaiseminen

Eksentristä anomaliaa ei voi ratkaista suljetussa muodossa Keplerin yhtälöstä. Yhtälö voidaan kuitenkin ratkaista helposti iteroimalla. Kirjoitetaan se aluksi muotoon

E = M + e sin E.

Kun eksentrisyys on pieni, keskianomalia ja eksentrinen anomalia ovat likimain samoja. Arvataan siis E₀ = M ja sijoitetaan yhtälön oikealle puolelle. Yhtälöstä voidaan nyt laskea uusi tarkempi E :n arvo:

E₁ = M + e sin E₀.

Tätä toistetaan, kunnes E :n arvot eivät enää muutu.

Lasketaan esimerkin vuoksi Jupiterin eksentrinen anomalia 23.8.1996, jolloin sen M = 277.7940° = 4.8484 rad. Jupiterin radan eksentrisyys on e = 0.0484.

E₀ = M = 4.8484,
E₁ = M + e sin E₀ = 4.8004,
E₂ = M + e sin E₁ = 4.8002,
E₃ = M + e sin E₂ = 4.8002.

Koska tällä tarkkuudella peräkkäiset E :n arvot eivät enää muutu, on ratkaisu E = 4.8002 rad = 215.0°.

Suppeneminen on sitä hitaampaa, mitä suurempi on eksentrisyys. Suppenemista voidaan nopeuttaa valitsemalla alkuarvo hieman älykkäämmin. Useimpiin käytännön tarkoituksiin ylläoleva menetelmä on kuitenkin aivan riittävä.

Sarjakehitelmä

Eksentrinen anomalia voidaan kehittää potenssisarjaksi eksentrisyyden suhteen. Lasku johtaa ns. Besselin funktioihin, emmekä puutu siihen tässä. Jos mukaan otetaan korkeintaan eksentrisyyden kolmatta potenssia sisältävät termit, saadaan lauseke

E = M + e sin M + (e² / 2) sin 2M + (e³ / 8) (- sin M + 3 sin 3M).

Artikkelin alkuun

Erikieliset vastineet

Kepler's equation

englanti (English)

Käytetyt lähteet

Zubenelgenubi

Alaviitteet

Lähdeviittaus tähän sivuun:
Tieteen termipankki 5.12.2025: Tähtitiede:Keplerin yhtälö. (Tarkka osoite: https://tieteentermipankki.fi/wiki/Tähtitiede:Keplerin yhtälö.)

Siirry tarkastelemaan sivun muokkaushistoriaa →