Tähtitiede:neutronitähti
neutronitähti
| neutronitähti |
Tähden loppuvaiheisiin liittyy URCA-prosessi, jossa syntyy runsaasti neutriinoja aineen koostumuksen muuten muuttumatta. URCA-prosessissa tapahtuu reaktioita
(Z, A ) + e- -> (Z -1, A ) + elektronin neutriino
(Z -1, A ) -> (Z, A ) + e- + elektronin antineutriino,
missä Z on protonien määrä ytimessä, A massaluku (protonien ja neutronien määrä) ja e elektroni.
Elektronikaasun ollessa degeneroitunutta ei Paulin kieltosäännön nojalla uusia elektroneja pääse muodostumaan, joten jälkimmäinen reaktio estyy. Seurauksena on ytimien protonien muuttuminen neutroneiksi. Ytimien neutronisoituessa niiden sidosenergia samalla pienenee, kunnes tiheyksissä 4 × 1014 kg/m3 neutronit alkavat tihkua ulos ytimistä ja tiheyksissä 1017 kg/m3 ytimet ovat kokonaan kadonneet. Aine on neutronipuuroa, jonka seassa on puolisen prosenttia elektroneja ja protoneja.
Neutronitähdissä toimii gravitaatiota vastustavana voimana degeneroituneen neutronikaasun paine, samaan tapaan kuin valkeissa kääpiöissä elektronikaasun paine. Tilanyhtälökin on aivan samaa muotoa; elektronin massa on vain korvattava neutronin massalla ja keskimääräinen molekyylipaino vapaata elektronia kohti keskimääräisellä molekyylipainolla vapaata neutronia kohti $\mu_{\rm n}$. Koska kaasu koostuu lähes yksinomaan neutroneista, on $\mu_{\rm n} \approx 1$.
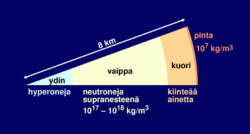
Neutronitähtien tyypilliset läpimitat ovat 10 km:n luokkaa. Neutronitähdillä on tavallisista tähdistä poiketen selvä kiinteä pinta. Sen yllä on korkeintaan parin senttimetrin vahvuinen atmosfääri. Pinnan yläosa on kiinteää metallimaista ainetta, jonka tiheys kasvaa nopeasti sisällepäin mentäessä. Suurin osa tähteä on neutroneista koostuvaa supranestettä, ja keskustassa, jossa tiheys ylittää 1018 kg/m3, voi olla raskaammista hiukkasista (hyperoneista) muodostunut mahdollisesti kiinteä ydin.
Supernovaräjähdyksessä ja -luhistumisessa syntyvä neutronitähti pyörii aluksi nopeasti, koska sen impulssimomentti on säilynyt ennallaan, mutta koko on paljon aiempaa pienempi. Parissa tunnissa tähti vakaantuu voimakkaasti litistyneeksi ellipsoidiksi, joka pyörähtää ympäri useita satoja kertoja sekunnissa. Myös neutronitähden alkuperäinen \ii{magneettikenttä} on luhistunut voimakkaaksi kentäksi, jolla tähti on kytkeytynyt ympärillä olevaan avaruuteen ja ainepilviin. Neutronitähden pyörimisenergia vähenee koko ajan tähden ja sen magneettisen ympäristön säteillessä sähkömagneettista säteilyä, \ii{neutriinoja}, \ii{kosmisia säteitä} (eli hiukkasia) ja mahdollisesti \ii{gravitaatiosäteilyä}. Siten pyöriminen hidastuu jatkuvasti. Pyöriminen voi myös hajottaa tähden useaksi erilliseksi kappaleeksi. Ne yhtyvät vähitellen takaisin, kun järjestelmän energia pienenee. Joissakin tapauksissa voivat tähdet jäädä myös erillisiksi, jolloin syntyy esimerkiksi kaksoisneutronitähtiä.
Neutronitähtien teoria kehitettiin jo 1930-luvulla, mutta ensimmäiset havainnot niistä tehtiin vasta 1960-luvulla. Silloin havaittiin taivaalla radioalueella sykkiviä \i{pulsareita}. 1970-luvulta alkaen neutronitähtiä on havaittu myös \i{röntgenpulsareina} ja \i{röntgenpurkautujina}.
\example a) Jos Aurinko kutistuisi 20 kilometrin säteiseksi neutronitähdeksi, mikä olisi sen tiheys?\nl b) Jos oletetaan Aurinko homogeeniseksi palloksi, jonka pyörähdysaika on 25 d, mikä olisi pyörähdysaika Auringon kutistuttua neutronitähdeksi? \noindent a) Neutronitähden tiheys olisi $$ \rho={M_\odot\over{4\over3}\pi R^3}= {2\times10^{30}\ {\rm kg}\over{4\over3}\pi(20\times10^3)^3\ {\rm m}^3} \approx 6\times10^{16}\ {\rm kg/m}^3. $$ Pyörähdysaika saadaan kuten esimerkissä 11.1: $$\eqalign{ P&=P_\odot\biggl({R\over R_\odot}\biggr)^2 \cr &=25\ {\rm d}\biggl({20\times10^3\over 6.96\times10^8}\biggr)^2\cr &=2.064\times10^{-8}\ {\rm d} \approx 0.0018\ {\rm s}. } $$ Neutronitähdeksi luhistunut Aurinko kieppuisi siis yli 550 kierrosta sekunnissa. \endex
\noindent {\bf\ii{Pulsarit}.} Pulsarit löydettiin 1967, kun Cambridgen yliopistossa Englannissa \i{Antony Hewish} ja \i{Jocelyn Bell} huomasivat taivaalta tulevia säännöllisiä radiomerkkejä. Sittemmin pulsareita on löydetty toistasataa. Nimensä ne ovat saaneet toistuvista, terävistä radiopulsseista, joiden väliaika vaihtelee 0.0016 sekunnista (pulsari \ii{1937 + 214}) useaan sekuntiin.
\fig{5.5cm}{\frame{0 0 11 5.2
Erikieliset vastineet
| neutron star | englanti (English) |
Alaviitteet
Lähdeviittaus tähän sivuun:
Tieteen termipankki 27.2.2026: Tähtitiede:neutronitähti. (Tarkka osoite: https://tieteentermipankki.fi/wiki/Tähtitiede:neutronitähti.)
{Pyörivää \ii{neutronitähteä} ympäröivä \ii{magneettikenttä} kuljettaa mukanaan \ii{plasmaa}. Tietyllä etäisyydellä plasman nopeus lähenee valon nopeutta, ja tällä etäisyydellä olevat säteilyalueet $S$ lähettävät säteilyä eteenpäin kapeaan kartioon. Pisteestä $P$ lähtevä säteily osuu havaitsijaan, joka on nuolen suunnassa. (Smith (1977): Pulsars, Cambridge University Press, 189)}
Säteilyn jaksossa esiintyy tasaisen pitenemisen lisäksi toisinaan nopeita pieniä hyppäyksiä. Koska pulssit syntyvät neutronitähden pyöriessä nopeasti akselinsa ympäri, merkitsee niiden väliajan kasvu pyörimisen hidastumista. Äkilliset muutokset saattavat merkitä massansiirroksia tähdessä (\ii{""tähdenjäristyksiä""}) tai sen lähiympäristössä.
Radiopulssien synty on yhteydessä neutronitähden voimakkaaseen \ii{magneettikenttään}, jonka akseli ei yhdy pyörimisakseliin, vaan muodostaa sen kanssa jopa 45--90 asteen kulman. Tähden ympärillä on \ii{magnetosfääri}, jossa hiukkaset pyörivät magneettikentän vankeina. Tietyllä etäisyydellä tähdestä pyörimisnopeus lähestyy valon nopeutta. Nopeasti liikkuva varaus lähettää säteilyä kapeaan kartioon. Kartio kiertää neutronitähden pyörimisnopeudella, ja säteily nähdään nopeina pulsseina sen pyyhkiessä ympäri majakan valon tavoin. Samalla neutronitähdestä virtaa ulospäin relativistisia hiukkasia.
\leftfig{8.3cm}{0cm}{7.5cm}{\frame{0 0 7 7}}{ Kahden \ii{pulsarin} peräkkäisiä radiopulsseja 408\break MHz taajuudella. Vasemmalla \ii{PSR 1642--03} ja oikealla \ii{PSR\break 1133+16}. Havainnot on tehty Jodrell Bankissa. (Smith: Pulsars, 93, 95)}
\fig{5.8cm}{\frame{0 0 5.4 5.5}\frame{5.7 0 11 5.5}}{% \ii{Rapusumun} pulsarin sykkiminen näkyvässä valossa. Vasemmalla pulsaria ei näy, oikealla näkyy. (Lick Observatory)}
\leftfig{9.3cm}{0cm}{8cm}{\frame{-2 0 7.5 9}}{ Jotkut pulsarit ovat\break kirkkaita gamma-\break säteilyn lähteitä.\break Keskellä \ii{Rapusumun} pulsari ja ylhäällä vasemmalla röntgenlähde \ii{Geminga}. Sen etäisyys on vain 100 pc, ja se on toistaiseksi lähin tunnettu röntgenlähde. (\ii{Compton Gamma Ray Observatory})\iii{gammasäteily}}
Tunnetuin pulsari liittyy \ii{Rapusumuun}. \ii{Härän} tähdistössä oleva pieni sumu kiinnitti ranskalaisen \i{Charles Messier'n} huomion 1700-luvun puolivälissä, ja siitä tuli Messier'n tunnetun luettelon ensimmäinen kohde \ii{M1}. Rapusumun havaittiin säteilevän voimakasta radiosäteilyä 1948, ja röntgensäteilyn lähteeksi se todettiin 1964. Vuonna 1968 löydettiin luhistumisessa syntynyt neutronitähti, kun havaittiin sen lähettämät nopeat, terävät radiopulssit. Seuraavana vuonna tähti löydettiin optisesti ja sen todettiin olevan myös röntgensäteilyn lähde.
Neutronitähtien havaitseminen on vaikeaa, koska niiden luminositeetti näkyvän valon aallonpituuksilla on erittäin pieni (tyypillisesti noin $10^{-6} L_\odot$). Tähän mennessä on Rapusumun neutronitähden lisäksi optisesti kyetty havaitsemaan mm.\ \ii{Velan} neutronitähti, jonka magnitudi kirkkaimmillaan on vain 25. Radioalueella se sen sijaan näkyy voimakkaana sykkijänä.
Yksinäisten pulsarien lisäksi on löydetty muutamia radioalueella säteileviä neutronitähtiä, jotka kuuluvat \ii{kaksoistähti}järjestelmiin. Näistä ensimmäinen, \ii{PSR 1913+16}, löytyi 1974. Sen löytämisestä palkittiin \i{Joseph Taylor} ja \i{Russell Hulse} vuonna 1993 Nobelin palkinnolla. Pulsari kiertää toista (ilmeisesti) neutronitähteä radalla, jonka eksentrisyys on 0.6 ja kiertoaika runsaat 8 h. Pulsarin pulssien väliajoista voidaan laskea \ii{Dopplerin siirtymän} perusteella pulsarin nopeuskäyrä. Havainnot saadaan hyvin tarkasti, ja niistä on voitu useiden vuosien ajan seurata järjestelmän rataelementtien muutoksia. \ii{Kaksoispulsarin} \ii{periastronin} suunnan on esimerkiksi havaittu kiertyvän eteenpäin noin $4\deg$ vuodessa. Tämä ilmiö voidaan selittää \ii{yleisen suhteellisuusteorian} avulla; aurinkokunnassa vastaava kiertymä on \ii{Merkuriuksella} 43 kaarisekuntia sadassa vuodessa.
\ii{Kaksoispulsari} \ii{PSR 1913+16} antaa todisteita myös \ii{gravitaatioaaltojen} olemassaolon puolesta. Järjestelmä on viiden havaintovuoden aikana menettänyt energiaa juuri niin paljon kuin sen yleisen suhteellisuusteorian mukaan olisi pitänyt säteillä gravitaatioaaltoina. Energianmenetys nähdään tähtien välimatkan ja kiertoajan pienenemisenä.
\fig{9.3cm}{\frame{0 0 11 9}}{\ii{Röntgenpulsarin} \ii{Hercules X-1} sykkimisessä näkyy selvä 1.24 sekunnin jakso. Havaintojen päälle on sovitettu niihin parhaiten sopiva käyrä. (Tananbaum et al.(1972): Astrophys. J. {\bf 174}, L 143)}
\fig{8.3cm}{\frame{0 0 11 8}}{Nopean röntgenpurkautujan eli \ii{""bursterin""} \ii{MXB 1730--335} röntgenryöppyjä. Kuvaan on merkitty 100 sekunnin aika. (Lewin (1977): Ann. N.Y. Academy of Sciences {\bf 302}, 310)}
\noindent {\bf\ii{Röntgenpulsarit}.} Röntgenalueella havaittiin 1970-luvulla monenlaisia muuttuvia tähtiä, joista röntgenpulsarit ja röntgenpurkautujat liittyvät neutronitähtiin. Röntgenpulsarit lähettävät sykkivää röntgensäteilyä. Niiden pulssien väliajat eivät kuitenkaan pitene kuten radiopulsareilla, vaan lyhenevät. Koska pulssien syntymekanismi on samantapainen kuin radioalueella, merkitsee jakson lyheneminen pulsarin pyörimisnopeuden kasvamista. Pulssien jaksot ovat röntgenpulsareilla oleellisesti pitemmät kuin radiopulsareilla, muutamasta sekunnista kymmeniin minuutteihin.
Röntgenpulsarit ovat aina komponentteja kaksoistähtijärjestelmässä. Tämä nähdään säteilyn säännöllisestä \ii{Dopplerin siirtymästä}. Seuralainen on tyypillisesti OB-spektriluokan ylijättiläinen. Kaksoistähtiluonne selittääkin röntgenpulsarien ominaisuudet. Röntgenpulsari syntyy kaksoistähtijärjestelmässä olevasta neutronitähdestä. Alkuun neutronitähti nähdään tavallisena radiopulsarina, jonka voimakas säteily estää naapuritähdestä vuotavan kaasun virtaamisen tähden lähelle. Pulsarin hidastuessa sen säteilemä energia kuitenkin vähenee. Lopulta seuralaisen tähtituuli pääsee tunkeutumaan neutronitähden magneettisille navoille, jolloin lähes valon nopeudella pintaan törmäävä massa säteilee röntgensäteilyä. Tähden pyöriessä säteilykartio pyyhkii taivaan yli ja säteily havaitaan pulsseina. Naapuritähdestä virtaava voimistunut tähtituuli saa neutronitähden pyörimisen nopeutumaan puhaltaessaan koko ajan samaan suuntaan neutronitähteä ympäröivään kiekkoon.
Tyypillinen nopea röntgenpulsari on \ii{Hercules X-1}, jonka säteilykäyrää näkyy kuvassa 14.7. Pulssit ovat jaksollisia ja jakson pituus on 1.24 s. Säteilylähde on komponenttina kaksoistähtijärjestelmässä, jonka ominaisuudet voidaan laskea havainnoista (tähti on pimennysmuuttuja). Esimerkiksi pulsarin massaksi saadaan noin yksi Auringon massa eli tyypillinen neutronitähden massa. Järjestelmä on tunnistettu optisella alueella näkyväksi muuttujaksi \ii{HZ Herculis}.
\noindent {\bf\ii{Röntgenpurkautujat}.} Röntgenpurkautujat eli \i{bursterit} ovat epäsäännöllisiä muuttujia, joissa kääpiönovien tavoin tapahtuu satunnaisia purkauksia. Purkausten väliaika on tyypillisesti tuntien tai vuorokausien luokkaa, mutta nopeampiakin purkautujia on tavattu. Purkauksen voimakkuus näyttää näilläkin riippuvan latautumisajan pituudesta. Röntgenpurkautujilla säteilylähde ei voi olla vedyn syttyminen, koska säteily on paljon kovempaa, sen huippuhan sattuu röntgenalueelle. Selitykseksi purkautujille on ehdotettu kääpiönovan kaltaista kaksoistähteä, jossa valkean kääpiön tilalla on neutronitähti. Seuralaisesta virtaa sen pinnalle lisämassaa, jonka vety palaa tähden pinnalla jatkuvasti heliumiksi. Kasvava heliumkuori saavuttaa lopulta kriittisen lämpötilan ja palaa heliumleimahduksessa hetkessä hiileksi. Koska tähdellä ei nyt ole laajoja vaimentavia ulkokuoria, leimahdus nähdään röntgenalueella esiintyvänä purkauksena.
Uskotaan, että myös \i{gammapurkaukset}, hyvin lyhyet ja terävät gammapulssit, liittyvät neutronitähtiin. \ii{Comptonin gammaobservatoriosatelliitilla} tehdyt havainnot ovat osoittaneet, että gammapurkaukset ovat jakautuneet taivaalle lähes tasaisesti, eivätkä siksi voi syntyä tavallisissa neutronitähdissä. Mahdollisesti kyseessä on muiden galaksien kaksoisneutronitähtien komponenttien yhteensulautuminen.
Kuten luvussa 11.5 nähtiin, neutronitähden massalla on yläraja, \ii{Oppenheimerin-Volkoffin massa}, jota raskaammissa tähdissä degeneroituneen neutronikaasun paine ei riitä vastustamaan gravitaation luhistavaa voimaa. Koska neutronitähden koossapysymiseen vaikuttaa neutronikaasun paineen lisäksi myös muita tekijöitä (mm. hiukkasten väliset vuorovaikutukset), on ylärajaa teoreettisesti vaikea laskea. Sen arvellaan kuitenkin olevan $M_{\rm OV} \approx 1.5-2 M_\odot$.
\null\vvv \boxi{Valkean kääpiön ja\nl neutronitähden säde}{7.6}
\noindent \ii{Valkean kääpiön} tai \ii{neutronitähden} massa määrää tähden säteen. Hydrostaattisen tasapainon yhtälön lisäksi on nyt nimittäin toinenkin ehto, degeneroituneen kaasun paineen riippuvuus tiheydestä. Hydrostaattisen tasapainon yhtälön (10.1), $$ {dP\over dr} = -{GM_r\rho\over r^2} $$ avulla voidaan arvioida keskimääräinen paine $P$: $$ {dP\over dr} \approx {P\over R} \propto {M \times M/R^3\over R^2} = {M^2 \over R^5}. $$ Tässä on sijoitettu $\rho \propto M/R^3$. Paineelle saadaan siis $$ P \propto {M^2/R^4}. \eqno\numbeq $$ \page \boxicont{20.6} Degeneroituneen elektronikaasun paineelle on ei-relativistisessa tapauksessa voimassa yhtälö (10.16): $$ P \approx (h^2/m_{\rm e}) (\mu_{\rm e} m_{\rm H})^{-5/3} \rho^{5/3}, $$ joten $$ P\propto {\rho^{5/3}\over m_{\rm e} \mu_{\rm e}^{5/3}}.\eqno\numbeq $$ Yhtälöistä (1) ja (2) saadaan $$ {M^2\over R^4} \propto {M^{5/3}\over R^5 m_{\rm e} \mu_{\rm e}^{5/3}} $$ eli $$ R \propto {1\over M^{1/3} m_{\rm e} \mu_{\rm e}^{5/3}} \propto M^{-1/3}. $$ Valkean kääpiötähden säde on siis sitä pienempi, mitä suurempi on sen massa. Jos tiheys kasvaa niin suureksi, että on käytettävä relativistista tilanyhtälöä (10.17), saadaan $$ P \propto \rho^{4/3} \propto {M^{4/3}\over R^4}. $$
Tähden kutistuessa kasvaa kaasun paine nyt samaa vauhtia hydrostaattisen tasapainon edellyttämän paineen (1) kanssa, eikä kerran alkanut luhistuminen pääty, ennen kuin aineen olomuoto muuttuu: elektronit ja protonit yhtyvät, ja syntyy neutronitähti. Vain riittävän massiivinen tähti saa aikaan rela
|kuvat= |tieteellinen nimi= |lähteet= |tarkistettu=Y |lisätiedot_fi= |luokka= |ilmiön kuvaus=N |logotiedosto= |logolinkki= |lähdeaineisto= }}